これは、2連続のブログポストの2つ目です。

概要

前回は、属性ベース証明書を利用した認証の仕組みと、なぜ Signal のような匿名ウェブアプリケーションが注目されているのかについて解説しました。

今回は、 Signal がどのように匿名証明書を利用してグループチャットの匿名性を担保しているのかについて解説します。

なお、ここで解説している内容はこちらの論文で読むこともできます。

最後に、このような仕組みがなぜ今後のIT システム全般にとって重要になるのかについても述べるので、技術的な話題に興味がない人は最後だけ読んでください。(今回はかなり専門的な内容になります。)

グループチャットの匿名性

ユーザーが、アプリケーション上で複数人のグループを作る場合、その情報をサーバーで保存しておくのが一般的です。

セキュリティのため、認証を行なって自分がそのグループに属すことを証明しなければ、ユーザーはグループの情報を取得できません。

このようなシステムの問題点は、サーバーが悪意のあるユーザーをグループに追加しても、ユーザーからはその検証が難しいという点にあります。

この問題点を防ぐため、ユーザーがユニークな公開鍵を準備し、公開鍵に複数のユーザー・Web サービスが承認することで、意図した公開鍵へのメッセージ送信が、意図したユーザーへの送信になることを保障したのが keybase です。

これは、メッセージの秘匿性を守る上では優れた方法ですが、1. アプリケーションにおけるユーザーとその他の SNS の主体が必ず結びついてしまうこと。 2. どのユーザー同士がグループを作ってしまっているかがわかること。から、匿名性の観点からは改善の余地があります。

誰がグループを作っているのかをサーバーから隠したいような場合、従来はサーバーに一切情報を持たせずユーザーの端末同士にグループの状態を持たせるという手法がありましたが、これの場合は認証と状態の整合性管理が難しいという難点がありました。

そこで、新しい Signal のプロトコルではグループの情報を暗号化した状態でサーバーに保持しつつ、そのグループに関する権限を匿名証明書で与えるというアプローチを取っています。

Signal による匿名証明書の利用方法

前提知識

以下では離散対数問題をとくのが難しい楕円曲線郡 $\mathbb{G}$上の要素を大文字、その郡の位数と同じ要素数の整数群 $\mathbb{Z}$ 上の要素を小文字で表します。

署名から MAC へ

前回述べたように、民間が勝手にサービスとして匿名証明書を使う場合、署名者 = 検証者であるという仮定を置くことができます。

このような場合、署名や暗号化に用いる鍵と、検証や復号に用いる鍵が同一であると仮定することができます。つまり共通鍵暗号です。

共通鍵暗号において、署名に相当するものは、 MAC (Message Authentication Code) と呼ばれます。

コミュニケーションプロトコルでよく使われる MAC は HMAC と呼ばれ、暗号学的ハッシュ関数を用いた単純なものですが、匿名証明書に用いる場合は代数学的 MAC (Algebraic MAC, AMAC) と呼ばれるものを使います。

これは、 Hash 関数の代わりに、楕円曲線状の点の乗算を用いたものです。

証明書に署名の代わりに AMAC を用いることで、検証者を限定する代わりにパフォーマンス面で数倍から数十倍のの向上が見込めます。

具体的には以下のようにして計算します
認証対象となる属性を $m_1$, $m_2$ とした時

属性の数 + 1だけランダムな値 $x_0$, $x_1$ $x_2$ を作成し、これを秘密鍵とする。
適当な楕円曲線上の点 $U$ を準備する。これは誰も離散対数を知らない点 (NUMS) でも良いが、作成者が離散対数を知っているような点でも良い。その場合、離散対数は作成者のみが知っているようにすること
$ T = (x_0 + m_1 * x_1 + m_2 * x_2) * U$ を計算し、($U$, $T$)を MAC とする。

メッセージの長さが、楕円曲線の位数に対応している必要があるため、メッセージが長くなりすぎる場合分割数を増やす必要があります。

直感的な理解として大事なのは、通常の属性ベース証明書が楕円曲線上の乗算を大量に行う必要があるのに対し、 MAC の場合は一度だけで良い。という点にあります。
楕円曲線の乗算はかなり CPU-heavy な計算なので、これによりかなり計算量を削減できます。

通常、検証は $(U, T)$ を受け取った時に
$T = (x_0 + m_1 * x_1 + m_2 * x_2) * U$
となることをチェックしますが、匿名証明書の場合、これだけでは以下の理由から不十分です。

証明書を受け取ったユーザーは、それが意図したメッセージに対するものであるか確認できない。
証明書を受け取ったユーザーは、それが適切なサーバーから発行されたものであるか検証できない。
検証者 (= 発行者) がメッセージ $m_l$ の値を知る必要がある。
証明書が発行時と提示時で同じなので、検証者が自分の発行した値を覚えておけばどのユーザーがリクエストしているのかわかってしまう

これらの問題を防ぐため、ゼロ知識証明を使います。

離散対数のゼロ知識証明

楕円曲線暗号では

適当な楕円曲線状の点に対する離散対数を知っていること
そのような隠された離散対数同士が任意の線形等式を満たすこと

を効率的にゼロ知識証明する手法が確立されています。

例えば、 $X_g = x * G$, $X_h = x * H$
という値を計算して、 $X_g$, $X_h$ を相手に渡したとします。
渡した二つの点が、同じ対数離散対数 $x$ から作られたものであることを ($x$ を隠しつつ)証明したい場合、まずランダムな $k$ を作成し、以下を計算してから

$R_g = k * G, R_h = k * H$
$c = Hash(R_g || R_h || X_g || X_h)$
s = $k + c * x$

$(s, c)$ を相手に渡すというものです。
(検証は省略)

このようなゼロ知識証明をいちいち記述していたら長いので、以下のように簡略化して書きます。

$ PK\{(x, y): X_g = x * G \land X_h = y * H \land x = y \} $

これは、「 x と y という離散対数を知っており、かつそれらが同一である」ということに対する証明という意味です。

このような記法を Camenisch-Stadler 記法と呼びます。

Keyed Verification Anonymous Credential (KVAC)

こちらの論文で $MAC_{GGM}$ として解説されている内容です。

証明書の発行

まず、発行者が上記の手法で MAC を計算します。初めは発行者がメッセージの内容を知っているケースについて解説します。単純化のため、メッセージの数は二つであると仮定します。

証明書の実体は単なるメッセージに対する MAC、つまり $(U, T)$ ですが、ユーザーはこれが有効なものであることを検証する必要があるので、
$T = U * (x_0 + m_1 * x_1 + m_2 * x_2)$ が成り立つことを (秘密鍵 $x_0$, $x_1$, $x_2$ を隠したまま)証明するためのゼロ知識証明を追加します。

まず、発行者の公開鍵を以下のように計算し、あらかじめ周知しておきます。

$C_{x_0} = x_0 * G + r * H$
$X_1 = x_1 * G$
$X_2 = x_2 * G$

($x_0$ だけ公開鍵の形式が違うのは、セキュリティを証明する上でこのほうが都合が良いからです。深く理解したい場合はこちらの 2.3 説を参照)

その後、以下のゼロ知識証明を発行時に追加します。
$$
\pi := PK\{ (x_0, x_1, x_2, r) : T = U * (x_0 + m_1 * x_1 + m_2 * x_2 ) \land C_{x_0} = G * x_0 + H * r \land X_1 = x * G \land X_2 = x_2 * G \}
$$

追記: LN 支払いに応じた発行

発行時に Lightning Network で証明書を購入するようなスキームを提案しました。
これは、証明書の目的によって複数の観点から捉えることができます。

1. スパムリクエストの防止
- ユーザーが匿名かつ証明書が無料のままだと、使う予定のない証明書を大量にリクエストしてサーバーを落とす事ができます。private LN channel を介して支払いを受け付けることで、server はそのような攻撃を完全に防ぐことができます
- 「ユーザーが支払いをする直前で処理を止める」という攻撃ベクターがまだ残っていますが、その場合はその channel を閉じるか無視すれば OK です。
1. Atomic Swap
- 証明書が Stable Coin などの数的トークンをエンコードする場合、これはトラストフルなトークンと BTC の atomic swap とみなせます。
1. 支払いによる認証
- Signal のように証明書がユーザー認証に使われるものである場合、これは LSAT の変種とみなせます。
- Macaroon ベースの LSAT に比べて、以下のような Pro/Con があります。
- Pro
  - 匿名性 (Multi-show unlinkability)
  - サーバーが検証処理のみを行うエンドポイントを準備すれば、他人にトラストレスに権利を転売することができる。
- Con
  - 計算量が多い
  - Non-Interactive Restrictive Delegation ができない (つまり、サーバーと通信なしに自分の権利の一部を誰かにわけたり売ったりできない)

なおこの仕組みには Taproot とその後に続く LN のアップデートが必須です。

属性を発行者から隠す

では属性を発行者から隠す場合、どのようにしたらよいでしょうか?

$m$ を発行者に教える代わりに、 $M = m * G$ を教えれば $m$ の値を知らせずに済むように思います。
$U$ を NUMS ではなく、発行者が秘密鍵を知っている値 $U = b * G$ にすれば、$m$ ではなく $M$ から証明書 $(U, T)$ が計算できるためです
$T = U * (x_0 + x_1 * m_1 + x_2 * m_2) = b * (x_0 * G + x_1 * M_1 + x_2 * M _2)$

しかし、 $m$ はランダムな値ではないので、このままでは簡単にバレてしまいます。
(例えば年齢ならば、 $0 < m < 120$ なので、最大 120 回 $G$ で乗算すれば$M$ に一致する値が出てきてしまいます。)

通常このような場合は、適当な $r$ を生成してから $m * G + r * H$ を教えることで値を隠しますが、今回はそうすると証明書が計算できなくなります。

そこで、隠したい属性を ElGamal 暗号化してから、その暗号文を発行者に渡し、帰ってきてから復号します。
ElGamal 暗号は準同型性を持つので、暗号文のまま証明書を計算できるためです。

一般に、メッセージ $M = m * G$ に対する ElGamal 暗号は、適当な blinding factor $r$ をランダムに生成し
$(r * G, M + rP)$
とします。ただし $p, P = p * G$ が、ユーザーの秘密鍵・公開鍵ペアです。

復号は暗号文 $(c_1, c_2)$ を受け取った時に $c_1 - p * c_2$ で計算します。
暗号化は公開鍵を知っていれば誰でも行えますが、復号は秘密鍵 $p$ を知っている必要があります。

サーバーは秘密鍵を持っていないので、 $M$ (および $m$)の値を知ることができませんが、準同型性より、 $T$ の暗号文を計算することができます。暗号文のまま User に返し、 User が復号することで有効な証明書とします。

簡単のため、「適当な blinding factor $r$ を生成し、$r$ と公開鍵 $P$ から $M$ の ElGamal 暗号文を作成する関数」を $Enc_P(M)$
と記述します。

準同型性とは、以下が成り立つことを指します。

$$
Enc_P(A + B) = Enc_P(A) + Enc_P(B)
$$
$$
Enc_P(x * A) = x * Enc_P(A)
$$

$T$ の暗号文は
$Enc_P(T) = Enc_P(U * (x_0 + x_1 * m_1 + x_2 * m_2)) = Enc_P(U * x_0) + x_1 * b * (Enc_P(M_1) + Enc_P(M_2))$
になります。ここから $Enc_P(M_1)$ と $Enc_P(M_2)$ をユーザーから渡してもらえば、発行者は $Enc_P(T)$ を計算できることがわかります。

あとは、この $Enc_P(T)$ を User に返すとともに、これが適切に作られたものであることをゼロ知識証明すれば、 User は復号して有効な証明書を入手することができます。

このように属性を隠すことは一見あまり意味がないように思えます。(年齢を属性にした証明書を発行するならば、年齢を確認しないと意味がないのでは？)

実際には「別の証明書の内容を反映したKVAC証明書を作る」という大きな利点があります。例えば、 User が別の自治体に署名したもらった属性ベース証明書を持っている場合、「その年齢を隠したまま同じ年齢に対するそのサービス用の証明書を新たに発行してもらう」
といったことが可能で、これにより後から認証スキームを外部の仕組みと連携しつつパフォーマンスを損なわない仕組みが構築可能です。

証明書の提示

通常のゼロ知識証明では、まず証明書を渡し、それが自分の秘密鍵を含んでいることを証明しますが、今回は証明書をそのまま渡してしまうと、発行者が発行時に証明書を覚えていた場合に提示者を紐づけることができてしまいます。

そこで、証明書からさらに Commitment を作成し、その Commitment が有効な証明書のものであることをゼロ知識証明します。

もう少し具体的に言うと、例えば $m_1 + m_2 = 1$ の証明書を持っていることを証明したい場合、以下のようにします。

証明書を $(U_0, T_0)$ とする。
ランダムな blinding factor $\alpha, r, z_1, z_2$ を作成
ランダマイズした証明書を検証者に送る
- $U = \alpha * U_0$
- $T = \alpha * T_0$
証明対象となるメッセージへのコミットメントを作成し、検証者に送る
- $C_{m_1} = U * m_1 + G * z_1$
- $C_{m_2} = U * m_2 + G * z_2$
さらに、T 全体に対する commitment を計算して送信する。
- $ C_T = G * r + T$
最後に、これらが適切に構築されていることのゼロ知識証明を送る。$PK{ (\alpha, m_1, m_2, z_1, z_2, r) : U = \alpha * U_0 \land T = T_0 * \alpha \land m_1 + m_2 = 1 \land C_{m_1} = U * m_1 + G * z_1 \land C_{m_2} = U * m_2 + G * z_2 \land V = - G * r + X_1 * z_1 + X_2 * z_2 }$

$V$ と言う値が出てきていますが、検証者は blinding factor $z_1, z_2$ を知らなくても、 $V$ を再計算することができます。
$V = U * (x_0 + C_{m_1} * x_1+ C_{m_2} * x_2) - C_T$

これを用いてゼロ知識証明の検証に成功すれば、ユーザーは有効な証明書を持っているとわかります。

(原理としては、Diffie-Hellman 鍵交換で共有鍵を作るケースの応用です。ユーザーは blinding factor を、サーバーは秘密鍵をそれぞれ隠したまま、お互いにしか作れない共通の値を作り、それを使って自分の証明書にはサーバーの秘密鍵が含まれていることを (証明書を見せずに) 証明します。)

(私は初めてこれを読んだ時、よくこんな仕組みを思いつくなあ〜と感心しました。)

Signal での利用方法

KVAC への修正

Signal では上記の証明書のスキームに若干の変更を加えていますが、これは属性そのものを $\mathbb{Z}$ ではなく、 $\mathbb{G}$ 上の要素、つまり楕円曲線上の点にするためです。

これは一言で言うとパフォーマンスのためですが、もう少し詳しく説明します。

なぜ属性を楕円曲線上の点にしたいのかと言うと、属性自体を暗号化したまま扱えるようにしたいためです。例えばグループを作成する際そのグループに属するユーザーのID (UID) を一緒にサーバーに登録しますが、そのままではサーバーに UID がばれてしまうので、UID を暗号化したまま登録します。

ただ、どんな暗号化でも良いわけではなく、暗号文に対応する平文 UID に証明書が存在することを証明できる必要があります。そうしないと存在しないユーザーがグループに登録されてしまう可能性があるためです。

このような性質を持つ暗号文を検証可能暗号と呼びます。上記の ElGamal 暗号がその典型ですが、このような場合暗号文を $\mathbb{G}$ の要素にしないと、既存の楕円曲線暗号のテクニックが使えず、より複雑な暗号学的テクニック (Paillier 暗号など) を使う必要が出てくるので計算効率が格段に落ちてしまいます。

実際には Signal では ElGamal 暗号に類似の別の仕組みが使われています。これは、 ElGamal 暗号は特定の平文・秘密鍵に対して複数の暗号文が存在するためです。 (blinding factor と言う自由度があるため)、そうすると、同一のユーザーが複数同じグループに登録されてしまうような自体が起こってややこしいので、暗号文と平文が一対一であるような独自の仕組みを利用しています。

以上の理由により、Signal で利用される証明書は上記のものよりも複雑になっていますが、証明書の発行・提示などはほぼ同一の仕組みで行っているので、ここでは詳しい解説は省略します。

グループチャットへの応用

概観

一般に、チャットアプリケーションでは

全く関係のないユーザー
自分のプロファイルを閲覧できるユーザー
同じグループチャットに属するユーザー

の三つの関係性があります。

そこで、Alice と Bob という二人のユーザーがいるとして、Alice が Bob とまずお互いのプロファイルを観れるように、つまり友達として登録し、その後二人のグループチャットを作りたいとします。

匿名性の観点で重要なのは、このような処理を進めていく過程で、それぞれの処理の間の主体を紐付けられないようにすることです。

つまり、以下のような処理の流れがあったとして

Alice が自分の情報をサービスに登録する。
Alice が Bob に自分の情報を共有する。
Alice が Bob を含んだグループチャットを作る。
Alice がグループに変更を加える。

サーバーからみて Alice が毎回別人に見えるようにすることが重要です。
しかし、上記の処理は Alice 以外の人物が行えるようなものであってはいけません。(正確には 3, 4 は Bob が行っても良いのですが、単純化のため無視します。)

そのため、それぞれの段階で Alice や Bob に一定の権限を (匿名証明書の形式で) 渡します。
再度提示して権限を行使しても、 Server は誰が権限を行使しているのかわかりません。

グループの作成

全容を解説するのは大変なので、ここではいちばん重要な部分、すなわち Alice がユーザー登録し、自分を含むグループを作成する流れだけにとどめます。
以下の図にまとめました

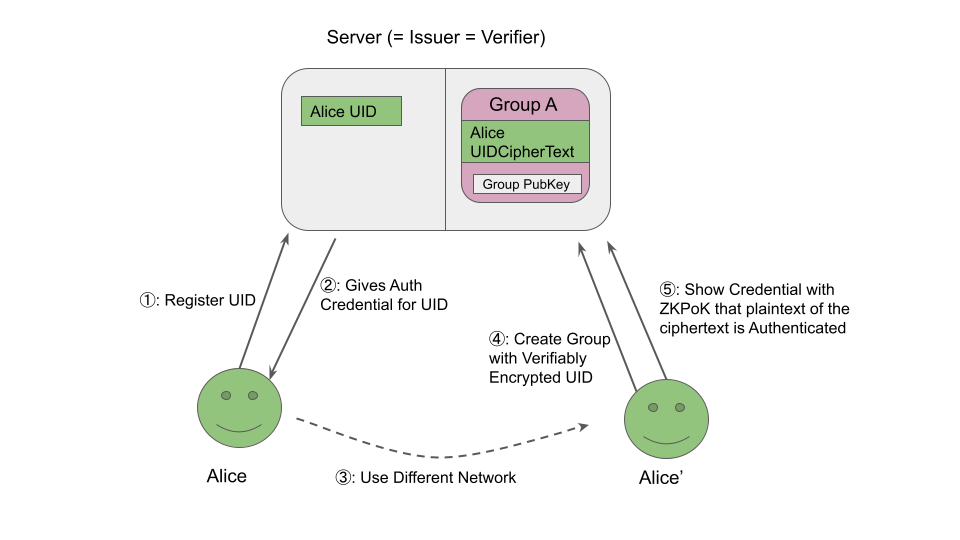
Server が、 Alice の UID とグループ内に存在する UID を紐付けられないよう、Alice は暗号化した UID をグループに登録しています。Server は暗号化した UID が既存の User のものであることを知る必要があるため、Alice は匿名証明書を提示してそのことを証明します。

Group 秘密鍵を知っていれば別のユーザーも同様の処理が行えるため、秘密鍵の共有によって、グループに inviite することができます。

まとめ: オープンソースからオープンプロトコルへ

Signal の仕組みは匿名証明書を営利サービスに応用する(おそらくは)最初の試みとして興味深いものです。

上記のプロトコルは複雑すぎて初めは完全な理解は難しいと思います。
しかし重要な点として認識しておきたいのは、サーバーは (自身の秘密鍵を除けば) 情報流出のリスクが一切ないという点です。

既存のサービスは、常に情報流出に対処するためのセキュリティコストを払う必要があります。これは、扱う情報が重要になるほど、そしてコンプライアンスを適切に行う社会的圧力が高まるほど高まるものです。

「適切にセキュアなサービスを運用するコストを、プロトコルの構築にかかるコストへと移行している」と考えれば、この複雑さにも納得がいくのではないでしょうか。

そして、この複雑さは (既存のサービスとは違い) 公に検証可能なものです。その点において、既存の金融システムをパブリックブロックチェーンへと移行させるのと同じモチベーションであるということができます。

業務用ソフトウェアをオープンソースにする運動は、様々な要因からその限界が見えつつあります。
プロトコルレベルでの検証可能性は、 (誰でもクライアントアプリケーションを作成できるので) ソフトウェアの OSS 化が必要ないという点で、このような潮流とも合致するものです。

欠点はマネタイズの難しさでしたが、前回の記事で述べたようにこれは暗号通貨によって解消される点です。

そして、これはちょっとあなたに考えてみて欲しいのですが、「サーバーが一定の条件に応じてユーザーに権利を与え、後ほどその権利をユーザーが行使する。」と言う仕組み自体は、既存のウェブサービス全てに当てはまるものです。

Netflix ... 月額課金と年齢認証に応じて、ユーザーに映像を見る権利を与え、ユーザーは後ほどそれを行使する。
Twitter ... 広告を提示する代わりに、ユーザーに1. テキストを投稿する権利、2.フォローしている && ブロックされていない相手の投稿を見る権利、3. 他のユーザーのプロフィールを見る権利 ... etc を与え、ユーザーはそれを必要な時に行使する。

したがって、広告や課金を LN 支払いで置き換えれば、ほぼ同じ機能でかつサーバーに対する匿名性の高いアプリケーションが構築できます。

欠点としては、 1. ユーザーの情報に基づいたコンテンツのレコメンデーションなどが難しくなる。 2. ユーザー端末の計算量 (したがって消費電力) が増える。といった点が挙げられるので、実際には全てを置き換えることはないでしょう。

実際のところ、匿名性を高めるスキームはチャットのような既存の応用例よりもこのようなデメリットを上回るメリットが存在するような新しい領域でこそ真価を発揮するものです。

例えば、Wasabi Wallet という名のビットコイン Wallet はすでに同じ仕組みを CoinJoin への参加の権利のトークンとして活用するプロトコルを検討しています。

より一般にいうと、この仕組みは金融・医療・公衆衛生などユーザーからみて匿名性が魅力的に映る事業領域で活用できる機会が多いものです。同時にこれらは(個人情報保護のため)民間法人が提供するのが難しかった領域でもあります。
こういった領域での web サービスを考えている方には Signal の仕組みには一考の余地があるのではないでしょうか。